Kód tohoto blogu je spolu s datovou sadou k dispozici na následujícím odkazu https: // github.com / shekharpandey89 / k-means
K-Means shlukování je algoritmus strojového učení bez dozoru. Pokud porovnáme algoritmus shlukování bez dohledu K-Means s supervizovaným algoritmem, není nutné trénovat model s označenými daty. Algoritmus K-Means se používá ke klasifikaci nebo seskupení různých objektů na základě jejich atributů nebo funkcí do K počtu skupin. Zde je K celé číslo. K-Means vypočítá vzdálenost (pomocí vzorce vzdálenosti) a poté najde minimální vzdálenost mezi datovými body a centroidním klastrem pro klasifikaci dat.
Pojďme pochopit K-Means pomocí malého příkladu pomocí 4 objektů a každý objekt má 2 atributy.
| Název_objektu | Atribut_X | Atribut_Y |
|---|---|---|
| M1 | 1 | 1 |
| M2 | 2 | 1 |
| M3 | 4 | 3 |
| M4 | 5 | 4 |
K znamená řešení numerického příkladu:
K vyřešení výše uvedeného numerického problému pomocí K-Means musíme postupovat podle následujících kroků:
Algoritmus K-Means je velmi jednoduchý. Nejprve musíme zvolit libovolné náhodné číslo K a poté zvolit centroidy nebo střed klastrů. Pro výběr centroidů můžeme pro inicializaci zvolit libovolný náhodný počet objektů (záleží na hodnotě K).
Základní kroky algoritmu K-Means jsou následující:
- Pokračuje v běhu, dokud se žádné objekty nepohnou ze svých středisek (stabilní).
- Nejprve náhodně vybereme některé centroidy.
- Poté určíme vzdálenost mezi každým objektem a centroidy.
- Seskupení objektů na základě minimální vzdálenosti.
Každý objekt má tedy dva body jako X a Y a představují v prostoru grafu následující:
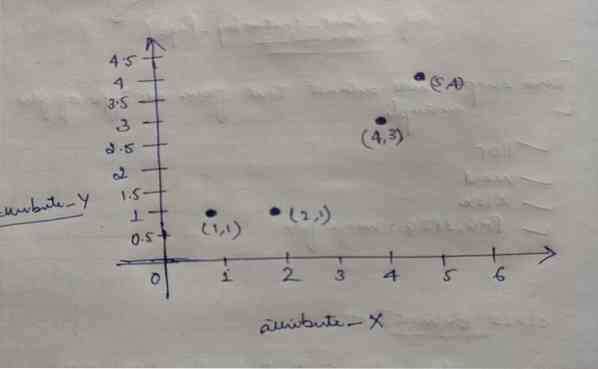
Abychom vyřešili náš výše uvedený problém, zpočátku zvolíme hodnotu K = 2 jako náhodnou.
Krok 1: Zpočátku jsme jako centroidy vybrali první dva objekty (1, 1) a (2, 1). Níže uvedený graf ukazuje to samé. Těmto centroidům říkáme C1 (1, 1) a C2 (2,1). Zde můžeme říci, že C1 je skupina_1 a C2 je skupina_2.
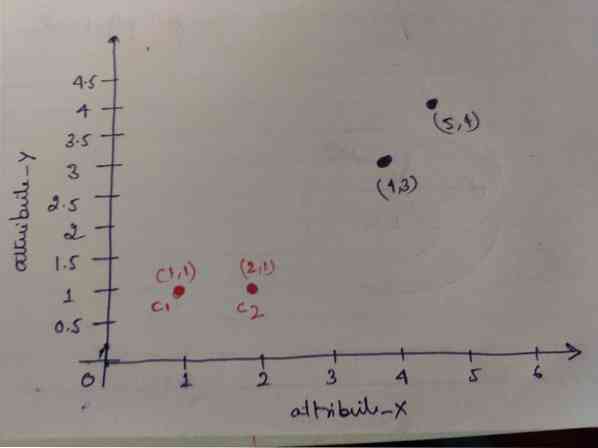
Krok 2: Nyní vypočítáme každý datový bod objektu na centroidy pomocí euklidovského vzorce vzdálenosti.
Pro výpočet vzdálenosti použijeme následující vzorec.

Vypočítáme vzdálenost od objektů k centroidům, jak je znázorněno na následujícím obrázku.

Takže jsme vypočítali vzdálenost každého datového bodu objektu pomocí výše uvedené metody vzdálenosti, nakonec jsme dostali matici vzdálenosti, jak je uvedeno níže:
DM_0 =
| 0 | 1 | 3.61 | 5 | C1 = (1,1) cluster1 | group_1 |
| 1 | 0 | 2.83 | 4.24 | C2 = (2,1) cluster2 | group_2 |
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | X |
| 1 | 1 | 3 | 4 | Y |
Nyní jsme vypočítali hodnotu vzdálenosti každého objektu pro každé těžiště. Například body objektu (1,1) mají hodnotu vzdálenosti k c1 je 0 a c2 je 1.
Protože z výše uvedené matice vzdálenosti zjistíme, že objekt (1, 1) má vzdálenost ke shluku1 (c1) je 0 a ke shluku2 (c2) je 1. Objekt je tedy blízko samotného clusteru1.
Podobně, pokud zkontrolujeme objekt (4, 3), vzdálenost ke shluku1 je 3.61 a cluster2 je 2.83. Takže objekt (4, 3) se přesune do clusteru2.
Podobně, pokud zkontrolujete objekt (2, 1), vzdálenost k clusteru 1 je 1 a ke clusteru 2 je 0. Tento objekt se tedy přesune na cluster2.
Nyní podle jejich hodnoty vzdálenosti seskupujeme body (shlukování objektů).
G_0 =
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | group_1 |
| 0 | 1 | 1 | 1 | group_2 |
Nyní podle jejich hodnoty vzdálenosti seskupíme body (shlukování objektů).
A nakonec bude graf vypadat níže po seskupení (G_0).
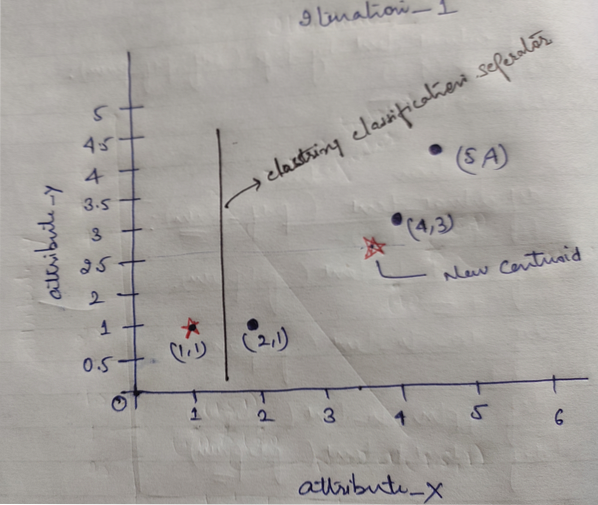
Iterace_1: Nyní budeme počítat nové centroidy, protože se počáteční skupiny změnily z důvodu vzorce vzdálenosti, jak je znázorněno v G_0. Takže skupina_1 má pouze jeden objekt, takže její hodnota je stále c1 (1,1), ale skupina_2 má 3 objekty, takže její nová hodnota těžiště je 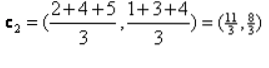
Takže nové c1 (1,1) a c2 (3.66, 2.66)
Nyní musíme znovu vypočítat celou vzdálenost k novým centroidům, jak jsme vypočítali dříve.
DM_1 =
| 0 | 1 | 3.61 | 5 | C1 = (1,1) cluster1 | group_1 |
| 3.14 | 2.36 | 0.47 | 1.89 | C2 = (3.66,2.66) cluster2 | group_2 |
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | X |
| 1 | 1 | 3 | 4 | Y |
Iteration_1 (shlukování objektů): Nyní jsme ji jménem nového výpočtu matice vzdáleností (DM_1) seskupili podle toho. Posuneme tedy objekt M2 ze skupiny_2 do skupiny_1 jako pravidlo minimální vzdálenosti na centroidy a zbytek objektu bude stejný. Nové shlukování bude tedy uvedeno níže.
G_1 =
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | group_1 |
| 0 | 0 | 1 | 1 | group_2 |
Nyní musíme znovu vypočítat nové centroidy, protože oba objekty mají dvě hodnoty.
Nové centroidy tedy budou 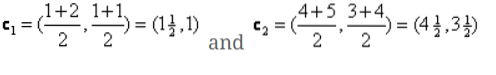
Poté, co získáme nové centroidy, bude shlukování vypadat níže:
c1 = (1.5, 1)
c2 = (4.5, 3.5)
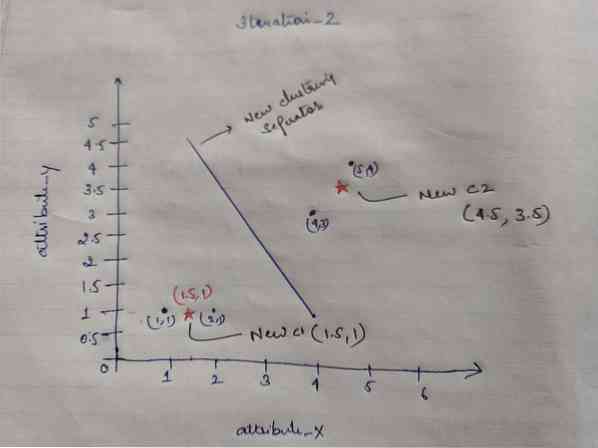
Iteration_2: Opakujeme krok, ve kterém vypočítáme novou vzdálenost každého objektu k novým vypočítaným centroidům. Po výpočtu tedy získáme následující matici vzdálenosti pro iteraci_2.
DM_2 =
| 0.5 | 0.5 | 3.20 | 4.61 | C1 = (1.5, 1) cluster1 | group_1 |
| 4.30 | 3.54 | 0.71 | 0.71 | C2 = (4.5, 3.5) cluster2 | group_2 |
ABECEDA
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | X |
| 1 | 1 | 3 | 4 | Y |
Opět děláme přiřazení klastrů na základě minimální vzdálenosti, jako jsme to dělali dříve. Poté jsme dostali shlukovací matici, která je stejná jako G_1.
G_2 =
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | group_1 |
| 0 | 0 | 1 | 1 | group_2 |
Jako tady, G_2 == G_1, takže není nutná žádná další iterace a my se zde můžeme zastavit.
Implementace K-Means pomocí Pythonu:
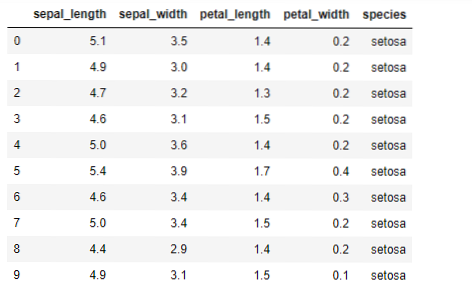
Nyní budeme implementovat algoritmus K-means v pythonu. K implementaci K-means použijeme slavnou datovou sadu Iris, která je open-source. Tato datová sada má tři různé třídy. Tato datová sada má v zásadě čtyři funkce: Sepální délka, šířka sepalu, délka okvětního lístku a šířka okvětního lístku. Poslední sloupec řekne název třídy daného řádku jako setosa.
Datová sada vypadá takto:
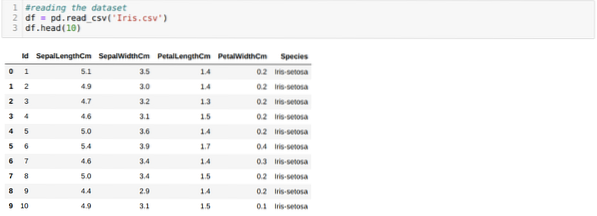
Pro implementaci pythonu k-means musíme importovat požadované knihovny. Takže importujeme Pandy, Numpy, Matplotlib a také KMeans ze sklearnu.clutser, jak je uvedeno níže:

Čteme Iris.csv datová sada pomocí metody read_csv panda a zobrazí prvních 10 výsledků pomocí metody head.
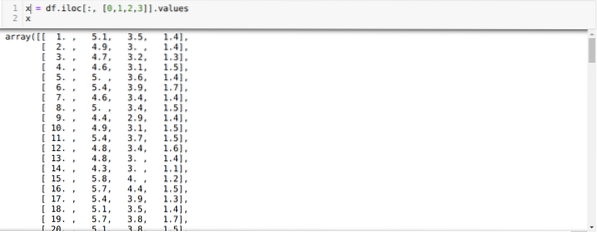
Nyní čteme pouze ty funkce datové sady, které jsme potřebovali k trénování modelu. Čteme tedy všechny čtyři funkce datových sad (délka sepalu, šířka sepalu, délka okvětního lístku, šířka okvětního lístku). Za tímto účelem jsme předali čtyři hodnoty indexu [0, 1, 2, 3] do funkce iloc datového rámce pandy (df), jak je znázorněno níže:
Nyní náhodně zvolíme počet klastrů (K = 5). Vytvoříme objekt třídy K-means a poté do ní vložíme naši x datovou sadu pro trénink a predikci, jak je znázorněno níže:
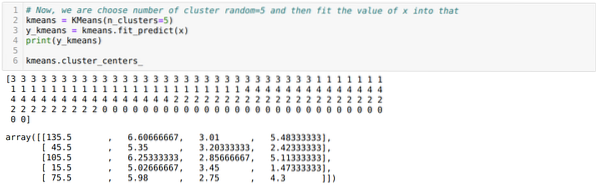
Nyní si představíme náš model s náhodnou hodnotou K = 5. Vidíme jasně pět shluků, ale vypadá to, že to není přesné, jak je znázorněno níže.
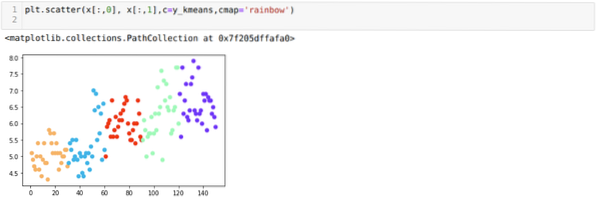
Naším dalším krokem je tedy zjistit, zda byl počet klastrů přesný nebo ne. A k tomu používáme metodu Elbow. Metoda Elbow se používá ke zjištění optimálního počtu klastru pro konkrétní datovou sadu. Tato metoda bude použita ke zjištění, zda byla hodnota k = 5 správná nebo ne, protože nedostáváme jasné shlukování. Poté přejdeme k následujícímu grafu, který ukazuje, že hodnota K = 5 není správná, protože optimální hodnota spadá mezi 3 nebo 4.
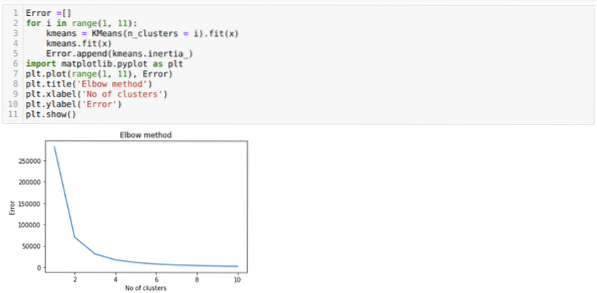
Nyní spustíme výše uvedený kód znovu s počtem klastrů K = 4, jak je znázorněno níže:
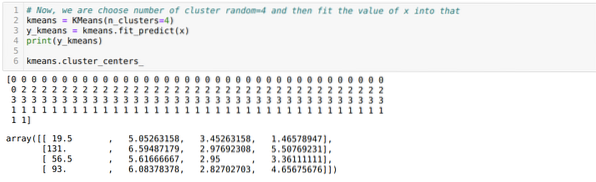
Nyní budeme vizualizovat výše uvedené seskupování nových sestavení K = 4. Níže uvedená obrazovka ukazuje, že nyní se shlukování provádí prostřednictvím k-means.
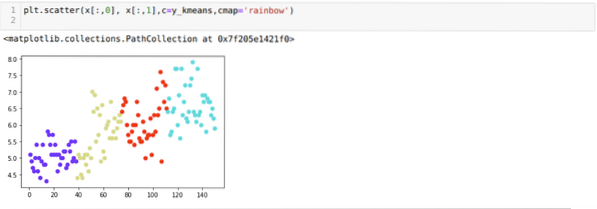
Závěr
Studovali jsme tedy algoritmus K-means v numerickém i pythonovém kódu. Také jsme viděli, jak můžeme zjistit počet klastrů pro konkrétní datovou sadu. Někdy metoda Elbow nemůže poskytnout správný počet klastrů, takže v takovém případě existuje několik metod, které si můžeme vybrat.
 Phenquestions
Phenquestions