Tak jako SciPy je otevřený zdroj, má velmi aktivní a živou komunitu vývojářů, díky které je k dispozici enormní množství modulů pro obrovské množství vědeckých aplikací a výpočtů dostupných v SciPy. Některé ze složitých matematických operací, které lze provádět pomocí SciPy, jsou:
- Interpolace
- Integrace
- Optimalizace
- Zpracovávání obrazu
- Statistika
- Výpočty speciálních funkcí atd.
SciPy lze srovnávat s většinou příkazových a standardních knihoven, jako je knihovna GSL pro C ++ a Matlab. Jelikož je SciPy postaven na balíčku NumPy, lze tyto dva balíčky také zcela integrovat. Pokud si můžete myslet na matematickou operaci, kterou je třeba provést, ujistěte se, že jste si před implementací tohoto modulu sami zkontrolovali knihovnu SciPy, protože ve většině případů má SciPy všechny operace pro vás plně implementované.
Nainstalujte si knihovnu SciPy
Pojďme si nainstalovat knihovnu SciPy, než přejdeme ke skutečným příkladům a konceptům. Existují dva způsoby instalace tohoto balíčku. První zahrnuje použití správce balíčků Pythonu, pip:
pip install scipyDruhý způsob se týká Anacondy, balíček můžeme nainstalovat jako:
conda install -c anaconda scipyJakmile je knihovna nainstalována, můžeme ji importovat jako:
importovat scipyNakonec, protože budeme používat také NumPy (Doporučuje se, aby pro všechny operace NumPy používali NumPy přímo místo procházení balíčkem SciPy):
importovat numpyJe možné, že v některých případech budeme také rádi vykreslovat naše výsledky, pro které použijeme knihovnu Matplotlib. Proveďte následující import pro tuto knihovnu:
import matplotlibU všech příkladů v této lekci budu používat správce Anaconda. Stejným způsobem spustím notebook Jupyter:

Nyní, když jsme připraveni se všemi dovozními příkazy napsat nějaký kód, pojďme se ponořit do balíčku SciPy s několika praktickými příklady.
Práce s polynomiálními rovnicemi
Začneme tím, že se podíváme na jednoduché polynomické rovnice. Existují dva způsoby, jak můžeme integrovat polynomiální funkce do našeho programu. Můžeme využít poly1d třída, která využívá koeficienty nebo kořeny polynomu pro inicializaci polynomu. Podívejme se na příklad:
z numpy import poly1dfirst_polynomial = poly1d ([3, 4, 7])
tisk (první_polynomial)
Když spustíme tento příklad, uvidíme následující výstup: When we run this example, we will see the following output:

Je zřejmé, že polynomická reprezentace rovnice je vytištěna jako výstup, takže výsledek je snadno srozumitelný. Můžeme provádět různé operace i na tomto polynomu, jako je kvadratura, nalezení jeho derivace nebo dokonce řešení pro hodnotu x. Zkusme to udělat v následujícím příkladu:
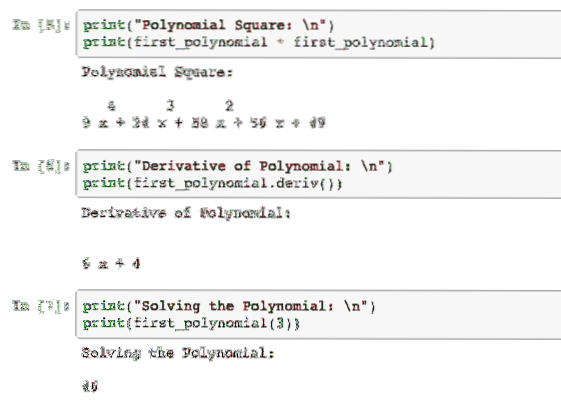
print ("Polynomiální čtverec: \ n")tisk (first_polynomial * first_polynomial)
print ("Derivace polynomu: \ n")
print (first_polynomial.deriv ())
print ("Řešení polynomu: \ n")
print (first_polynomial (3))
Když spustíme tento příklad, uvidíme následující výstup: When we run this example, we will see the following output:
Právě když jsem si myslel, že to je vše, co můžeme se SciPy dělat, vzpomněl jsem si, že můžeme integrovat také Polynomial. Pojďme spustit poslední příklad s Polynomials:
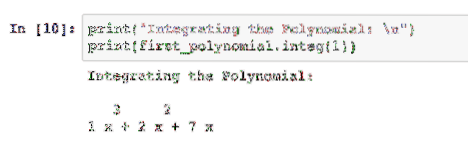
print ("Integrace polynomu: \ n")print (first_polynomial.integ (1))
Celé číslo, které předáme, říká balíčku, kolikrát má být polynom integrován:
Můžeme jednoduše předat další celé číslo, které říká balíčku, kolikrát má tento polynom integrovat.
Řešení lineárních rovnic
Je dokonce možné vyřešit lineární rovnice pomocí SciPy a najít jejich kořeny, pokud existují. Pro řešení lineárních rovnic reprezentujeme množinu rovnic jako pole NumPy a jejich řešení jako samostatná pole NumPy. Pojďme si to představit na příkladu, kde děláme totéž a využíváme linalg balíček k nalezení kořenů rovnic, zde jsou rovnice, které budeme řešit:
1x + 5y = 63x + 7y = 9
Vyřešme výše uvedené rovnice:
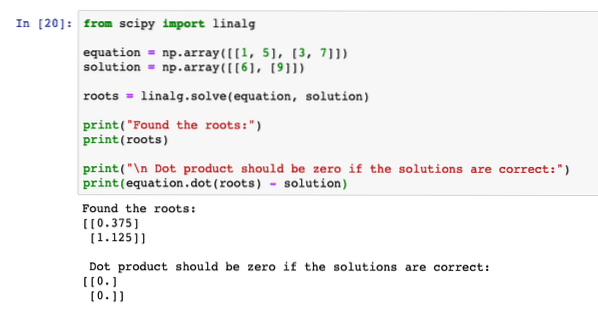
ze scipy import linalgrovnice = np.pole ([[1, 5], [3, 7]])
řešení = np.pole ([[6], [9]])
kořeny = linalg.řešit (rovnice, řešení)
print ("Nalezeny kořeny:")
tisk (kořeny)
print ("\ n Dot produkt by měl být nulový, pokud jsou řešení správná:")
tisk (rovnice.tečka (kořeny) - řešení)
Když spustíme výše uvedený program, uvidíme, že rovnice bodového produktu dává nulový výsledek, což znamená, že kořeny, které program našel, byly správné:
Fourierovy transformace se SciPy
Fourierovy transformace nám pomáhají vyjádřit funkci jako samostatné komponenty, které tuto funkci tvoří, a vede nás cestou, kterou můžeme tyto komponenty znovu zkombinovat a získat tak původní funkci zpět.
Podívejme se na jednoduchý příklad Fourierových transformací, kde pomocí knihovny Matplotlib vykreslíme součet dvou kosinů:
od scipy.fftpack importovat fft# Počet vzorkovacích bodů
N = 500
# mezery mezi vzorky
T = 1.0/800.0
x = np.linspace (0.0, N * T, N)
y = np.cos (50.0 * 2.0 * np.pi * x) + 0.5 * np.cos (80.0 * 2.0 * np.pi * x)
yf = fft (y)
xf = np.linspace (0.0, 1.0 / (2.0 * T), N // 2)
# matplotlib pro účely vykreslování
import matplotlib.pyplot jako plt
plt.spiknutí (xf, 2.0 / N * np.abs (yf [0: N // 2]))
plt.název ('Info')
plt.ylabel ('Y axis')
plt.xlabel ('X axis')
plt.mřížka()
plt.ukázat()
Zde jsme začali konstrukcí vzorového prostoru a kosinové rovnice, kterou jsme pak transformovali a vykreslili. Zde je výstup výše uvedeného programu:
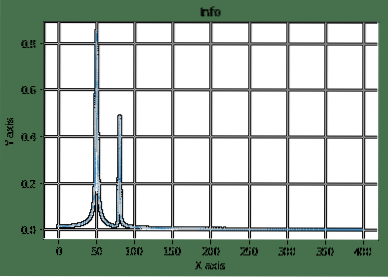
Toto je jeden z dobrých příkladů, kdy vidíme, že SciPy se používá ve složité matematické rovnici pro snadnou vizualizaci věcí.
Vektory a matice se SciPy
Nyní, když víme spoustu věcí, kterých je SciPy schopen, můžeme si být jisti, že SciPy může pracovat také s vektory a maticí. Matice jsou důležitou součástí lineární algebry, protože matice také používáme k reprezentaci vektorových mapování.
Stejně jako jsme se podívali na řešení lineárních rovnic pomocí SciPy, můžeme reprezentovat vektory s np.pole () funkce. Začněme konstrukcí matice:
my_matrix = np.matice (np.náhodný.náhodný ((3, 3)))tisk (my_matrix)
Zde je výstup výše uvedeného fragmentu:

Kdykoli mluvíme o maticích, vždy mluvíme o vlastních hodnotách a vlastních vektorech. Jednoduše řečeno, vlastní vektory jsou vektory, které po vynásobení maticí nemění svůj směr, na rozdíl od většiny vektorů. To znamená, že i když vynásobíte vlastní vektory maticí, existuje hodnota (nebo vlastní hodnota), která je jedním z faktorů násobení. To znamená:
Ax = λx.Ve výše uvedené rovnici je A matice, λ je vlastní hodnota a x je Vektor. Pojďme napsat jednoduchý fragment kódu, abychom našli vlastní čísla pro daný vektor:
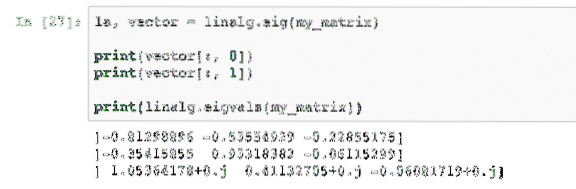
la, vektor = linalg.eig (my_matrix)tisk (vektor [:, 0])
tisk (vektor [:, 1])
tisk (linalg.eigvals (my_matrix))
Když spustíme tento příklad, uvidíme následující výstup: When we run this example, we will see the following output:
Výpočet determinantu matice
Další operací, kterou provedeme se SciPy, je výpočet determinantu 2-dimenzionální matice. Zde znovu použijeme matici, kterou jsme použili v posledním fragmentu kódu:
linalg.det (my_matrix)Když spustíme tento příklad, uvidíme následující výstup: When we run this example, we will see the following output:

Závěr
V této lekci jsme se podívali na mnoho dobrých příkladů, kde nám SciPy může pomoci tím, že pro nás provede složité matematické výpočty pomocí snadno použitelného API a balíčků.
 Phenquestions
Phenquestions


