Celkově se v této lekci budeme zabývat třemi hlavními tématy:
- Co jsou Tensors a TensorFlow
- Aplikování ML algoritmů s TensorFlow
- Případy použití TensorFlow
TensorFlow je vynikající balíček Pythonu od společnosti Google, který dobře využívá paradigma programování toku dat pro vysoce optimalizované matematické výpočty. Některé z funkcí TensorFlow jsou:
- Možnost distribuovaného výpočtu, která usnadňuje správu dat ve velkých sadách
- Hluboké učení a podpora neuronových sítí je dobrá
- Velmi efektivně spravuje složité matematické struktury, jako jsou n-dimenzionální pole
Díky všem těmto funkcím a řadě algoritmů strojového učení je TensorFlow implementací, což z ní dělá knihovnu produkčního měřítka. Pojďme se ponořit do konceptů v TensorFlow, abychom si mohli hned zašpinit ruce kódem.
Instalace TensorFlow
Protože budeme využívat Python API pro TensorFlow, je dobré vědět, že funguje s oběma Python 2.7 a 3.3+ verze. Pojďme si nainstalovat knihovnu TensorFlow, než přejdeme ke skutečným příkladům a konceptům. Existují dva způsoby instalace tohoto balíčku. První zahrnuje použití správce balíčků Pythonu, pip:
pip nainstalujte tensorflowDruhý způsob se týká Anacondy, balíček můžeme nainstalovat jako:
conda install -c conda-forge tensorflowNeváhejte hledat noční verze a verze GPU na oficiálních instalačních stránkách TensorFlow.
U všech příkladů v této lekci budu používat správce Anaconda. Stejným způsobem spustím notebook Jupyter:

Nyní, když jsme připraveni se všemi dovozními příkazy napsat nějaký kód, pojďme se ponořit do balíčku SciPy s několika praktickými příklady.
Co jsou tenzory?
Tenzory jsou základní datové struktury používané v Tensorflow. Ano, jsou to jen způsob, jak reprezentovat data v hlubokém učení. Pojďme si je zde představit:
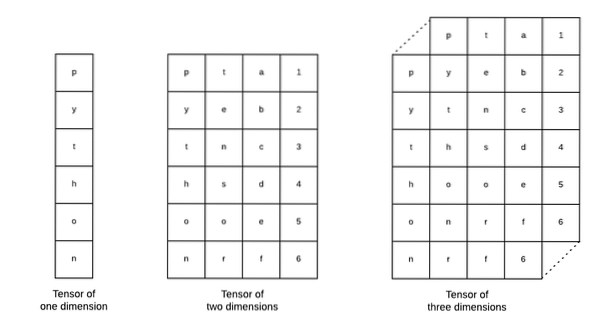
Jak je popsáno na obrázku, tenzory lze označit jako n-rozměrné pole což nám umožňuje reprezentovat data ve složitých dimenzích. Každou dimenzi můžeme v hlubokém učení považovat za jinou vlastnost dat. To znamená, že Tensors mohou vyrůst jako poměrně složité, pokud jde o složité datové sady s mnoha funkcemi.
Jakmile víme, co jsou Tensors, myslím, že je docela snadné odvodit, co se stane v TensorFlow. Tyto pojmy znamenají, jak v datových sadách mohou proudit tenzory nebo funkce, které produkují hodnotný výstup, když na něm provádíme různé operace.
Porozumění TensorFlow s konstantami
Jak jsme si přečetli výše, TensorFlow nám umožňuje provádět algoritmy strojového učení na Tensorech a vytvářet hodnotný výstup. S TensorFlow je návrh a trénink modelů Deep Learning přímočarý.
TensorFlow je dodáván s budovou Výpočetní grafy. Výpočtové grafy jsou grafy toku dat, ve kterých jsou matematické operace reprezentovány jako uzly a data jsou reprezentována jako hrany mezi těmito uzly. Napíšeme velmi jednoduchý fragment kódu, který poskytne konkrétní vizualizaci:
importovat tensorflow jako tfx = tf.konstantní (5)
y = tf.konstantní (6)
z = x * y
tisk (z)
Když spustíme tento příklad, uvidíme následující výstup: When we run this example, we will see the following output:
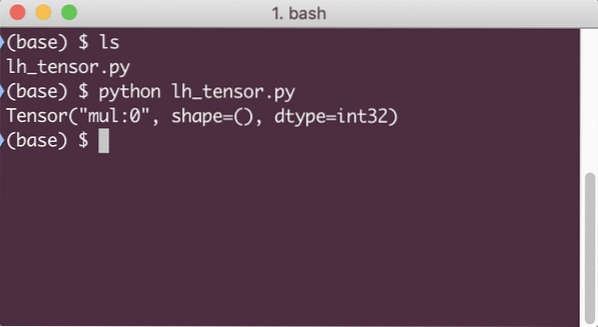
Proč je násobení špatné? To nebylo to, co jsme očekávali. Stalo se to proto, že takto nemůžeme provádět operace s TensorFlow. Nejprve musíme začít a zasedání aby výpočetní graf fungoval,
U relací můžeme zapouzdřit řízení provozu a stavu tenzorů. To znamená, že relace může také uložit výsledek výpočtového grafu, aby mohl tento výsledek předat další operaci v pořadí provedení potrubí. Vytvořme nyní relaci, abychom získali správný výsledek:
# Začněte s objektem relacerelace = tf.Zasedání()
# Poskytněte výpočet relaci a uložte ji
výsledek = relace.běh (z)
# Vytiskněte výsledek výpočtu
tisk (výsledek)
# Uzavřít relaci
zasedání.zavřít()
Tentokrát jsme relaci získali a poskytli jí výpočet, který potřebuje k běhu na uzlech. Když spustíme tento příklad, uvidíme následující výstup: When we run this example, we will see the following output:
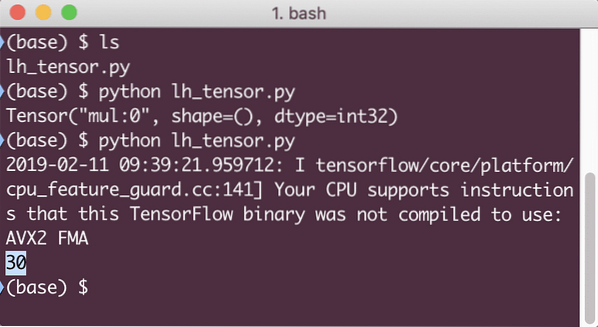
Přestože jsme obdrželi varování od TensorFlow, stále jsme dostali správný výstup z výpočtu.
Jednoprvkové tenzorové operace
Stejně jako to, co jsme v posledním příkladu znásobili dva konstantní Tensory, máme v TensorFlow mnoho dalších operací, které lze provést na jednotlivých prvcích:
- přidat
- odčítat
- násobit
- div
- mod
- břišní svaly
- záporný
- podepsat
- náměstí
- kolo
- čtv
- prášek
- exp
- log
- maximum
- minimální
- cos
- hřích
Single-element operations means that even when you provide an array, the operations will be done on each of the element of that array. Například:
importovat tensorflow jako tfimportovat numpy jako np
tenzor = np.pole ([2, 5, 8])
tenzor = tf.convert_to_tensor (tensor, dtype = tf.float64)
s tf.Session () jako relace:
tisk (relace.běh (tf.cos (tenzor)))
Když spustíme tento příklad, uvidíme následující výstup: When we run this example, we will see the following output:
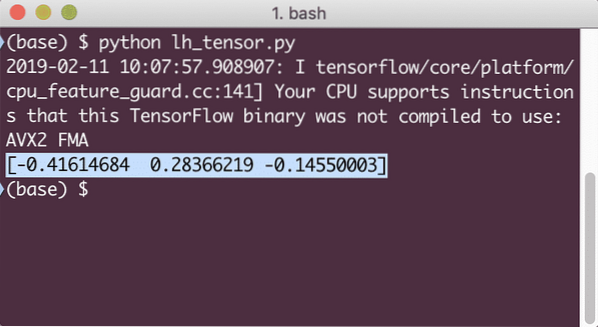
Pochopili jsme zde dva důležité pojmy:
- Libovolné pole NumPy lze snadno převést na Tensor pomocí funkce convert_to_tensor
- Operace byla provedena u každého z prvků pole NumPy
Zástupné symboly a proměnné
V jedné z předchozích částí jsme se podívali na to, jak můžeme použít konstanty Tensorflow k vytváření výpočetních grafů. Ale TensorFlow nám také umožňuje přijímat vstupy za běhu, takže výpočetní graf může mít dynamickou povahu. To je možné pomocí zástupných symbolů a proměnných.
Ve skutečnosti zástupné symboly neobsahují žádná data a musí být za běhu poskytnuty platné vstupy a podle očekávání bez zadání vygenerují chybu.
Zástupný symbol lze v grafu označit jako dohodu, že za běhu bude jistě poskytnut vstup. Zde je příklad zástupných symbolů:
importovat tensorflow jako tf# Dva zástupné symboly
x = tf. zástupný symbol (tf.float32)
y = tf. zástupný symbol (tf.float32)
# Přiřazení operace násobení w.r.t. A & b do uzlu mul
z = x * y
# Vytvořte relaci
relace = tf.Zasedání()
# Předejte hodnoty pro placehollders
výsledek = relace.běh (z, x: [2, 5], y: [3, 7])
print ('Násobení x a y:', výsledek)
Když spustíme tento příklad, uvidíme následující výstup: When we run this example, we will see the following output:
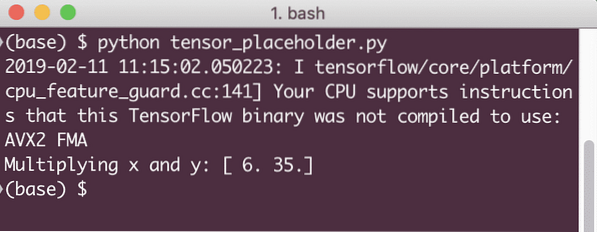
Nyní, když máme znalosti o zástupných symbolech, se zaměřme na Variables. Víme, že výstup rovnice se může v průběhu času měnit pro stejnou sadu vstupů. Když tedy trénujeme naši proměnnou modelu, může časem změnit své chování. V tomto scénáři nám proměnná umožňuje přidat tyto trénovatelné parametry do našeho výpočetního grafu. Proměnnou lze definovat takto:
x = tf.Proměnná ([5.2], dtype = tf.float32)Ve výše uvedené rovnici je x proměnná, která poskytuje svoji počáteční hodnotu a datový typ. Pokud neposkytneme datový typ, odvodí jej TensorFlow s jeho počáteční hodnotou. Zde se podívejte na datové typy TensorFlow.
Na rozdíl od konstanty musíme pro inicializaci všech proměnných grafu zavolat funkci Pythonu:
init = tf.global_variables_initializer ()zasedání.spustit (init)
Než použijeme náš graf, nezapomeňte spustit výše uvedenou funkci TensorFlow.
Lineární regrese s TensorFlow
Lineární regrese je jedním z nejběžnějších algoritmů používaných k navázání vztahu v daných kontinuálních datech. Tento vztah mezi souřadnými body, řekněme xay, se nazývá a hypotéza. Když mluvíme o lineární regrese, hypotéza je přímka:
y = mx + cZde m je sklon přímky a zde je to vektor představující závaží. c je konstantní koeficient (průsečík y) a zde představuje Zaujatost. Hmotnost a předpětí se nazývají parametry modelu.
Lineární regrese nám umožňuje odhadnout hodnoty hmotnosti a zkreslení tak, že máme minimum nákladová funkce. Nakonec x je nezávislá proměnná v rovnici a y je závislá proměnná. Nyní pojďme začít stavět lineární model v TensorFlow pomocí jednoduchého fragmentu kódu, který vysvětlíme:
importovat tensorflow jako tf# Proměnné pro sklon parametru (W) s počáteční hodnotou 1.1
W = tf.Proměnná ([1.1], srov.float32)
# Proměnná pro zkreslení (b) s počáteční hodnotou -1.1
b = tf.Proměnná ([- 1.1], srov.float32)
# Zástupné symboly pro zadání vstupu nebo nezávislé proměnné, označené x
x = tf.zástupný symbol (tf.float32)
# Rovnice přímky nebo lineární regrese
linear_model = W * x + b
# Inicializace všech proměnných
relace = tf.Zasedání()
init = tf.global_variables_initializer ()
zasedání.spustit (init)
# Proveďte regresní model
tisk (relace.běh (linear_model x: [2, 5, 7, 9]))
Zde jsme udělali přesně to, co jsme vysvětlili dříve, pojďme to shrnout zde:
- Začali jsme importem TensorFlow do našeho skriptu
- Vytvořte několik proměnných, které představují váhu vektoru a zkreslení parametrů
- K reprezentaci vstupu bude zapotřebí zástupný symbol, x
- Představují lineární model
- Inicializujte všechny hodnoty potřebné pro model
Když spustíme tento příklad, uvidíme následující výstup: When we run this example, we will see the following output:
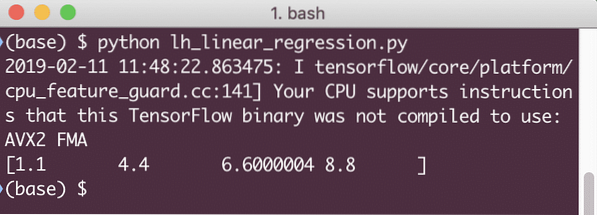
Jednoduchý fragment kódu poskytuje pouze základní představu o tom, jak můžeme vytvořit regresní model. K dokončení modelu, který jsme postavili, však musíme udělat ještě několik kroků:
- Musíme udělat náš model samoučitelný, aby mohl produkovat výstup pro všechny dané vstupy
- Musíme ověřit výstup poskytovaný modelem porovnáním s očekávaným výstupem pro dané x
Ztráta funkce a ověření modelu
K ověření modelu potřebujeme mít míru míry odchylky aktuálního výstupu od očekávaného výstupu. Existují různé funkce ztráty, které lze zde použít k ověření, ale podíváme se na jednu z nejběžnějších metod, Součet čtvercových chyb nebo SSE.
Rovnice pro SSE je uvedena jako:
E = 1/2 * (t - y) 2Tady:
- E = střední kvadratická chyba
- t = přijatý výstup
- y = očekávaný výstup
- t - y = chyba
Nyní napíšeme fragment kódu v návaznosti na poslední fragment, aby odrážel hodnotu ztráty:
y = tf.zástupný symbol (tf.float32)chyba = linear_model - r
squared_errors = tf.čtverec (chyba)
ztráta = tf.redukovat_součet (čtvercové chyby)
tisk (relace.běh (ztráta, x: [2, 5, 7, 9], y: [2, 4, 6, 8]))
Když spustíme tento příklad, uvidíme následující výstup: When we run this example, we will see the following output:
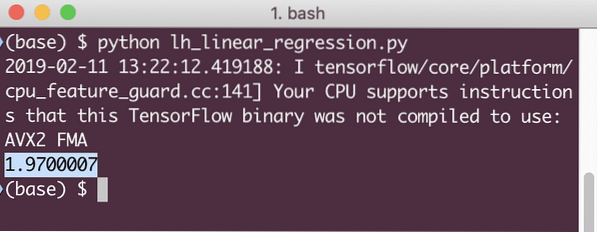
Je zřejmé, že hodnota ztráty je pro daný model lineární regrese velmi nízká.
Závěr
V této lekci jsme se podívali na jeden z nejpopulárnějších balíčků Deep Learning and Machine Learning, TensorFlow. Také jsme vytvořili lineární regresní model, který měl velmi vysokou přesnost.
 Phenquestions
Phenquestions


