Knihovna NumPy nám umožňuje provádět různé operace, které je třeba provést na datových strukturách často používaných v Machine Learning a Data Science, jako jsou vektory, matice a pole. Ukážeme pouze nejběžnější operace s NumPy, které se používají v mnoha kanálech Machine Learning. Nakonec si všimněte, že NumPy je jen způsob, jak provádět operace, takže matematické operace, které ukazujeme, jsou hlavním zaměřením této lekce a ne samotný balíček NumPy. Začněme.
Co je to Vector?
Podle Google je vektor veličina, která má směr i velikost, zejména pro určení polohy jednoho bodu v prostoru vzhledem k druhému.
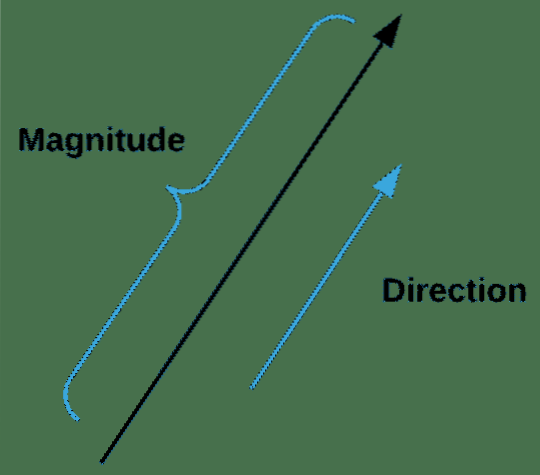
Vektory jsou ve strojovém učení velmi důležité, protože nepopisují pouze velikost, ale také směr funkcí. V NumPy můžeme vytvořit vektor pomocí následujícího fragmentu kódu:
importovat numpy jako nprow_vector = np.pole ([1,2,3])
tisk (řádek_vektor)
Ve výše uvedeném fragmentu kódu jsme vytvořili vektor řádku. Můžeme také vytvořit vektor sloupce jako:
importovat numpy jako npcol_vector = np.pole ([[1], [2], [3]])
tisk (col_vector)
Vytvoření matice
Matici lze jednoduše chápat jako dvourozměrné pole. Můžeme vytvořit matici s NumPy vytvořením vícerozměrného pole:
matice = np.pole ([[1, 2, 3], [4, 5, 6], [7, 8, 9]])tisk (matice)
I když je matice přesně podobná vícerozměrnému poli, maticová datová struktura se nedoporučuje ze dvou důvodů:
- Pole je standardem, pokud jde o balíček NumPy
- Většina operací s NumPy vrací pole a ne matici
Pomocí řídké matice
Připomínáme, že řídká matice je ta, ve které je většina položek nulová. Nyní je běžným scénářem ve zpracování dat a strojovém učení zpracování matic, ve kterých je většina prvků nulová. Zvažte například matici, jejíž řádky popisují každé video na Youtube a sloupce představují každého registrovaného uživatele. Každá hodnota představuje, pokud uživatel sledoval video nebo ne. Většina hodnot v této matici bude samozřejmě nulová. The výhoda s řídkou maticí je to, že neukládá nulové hodnoty. Výsledkem je obrovská výpočetní výhoda a optimalizace úložiště.
Vytvořme zde jiskrovou matici:
ze scipy importovat řídceoriginal_matrix = np.pole ([[1, 0, 3], [0, 0, 6], [7, 0, 0]])
sparse_matrix = řídký.csr_matrix (original_matrix)
tisk (sparse_matrix)
Abychom pochopili, jak kód funguje, podíváme se na výstup zde:
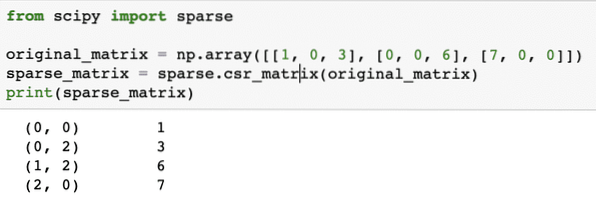
Ve výše uvedeném kódu jsme k vytvoření a použili funkci NumPy Stlačený řídký řádek matice, kde jsou nenulové prvky reprezentovány pomocí indexů založených na nule. Existují různé druhy řídké matice, například:
- Stlačený řídký sloupec
- Seznam seznamů
- Slovník klíčů
Nebudeme se zde potápět v jiných řídkých matricích, ale víme, že každá z jejich použití je specifická a nikdo nemůže být označen jako „nejlepší“.
Uplatnění operací na všechny prvky Vector
Jedná se o běžný scénář, když potřebujeme použít společnou operaci na více vektorových prvků. To lze provést definováním lambda a jeho vektorizací. Podívejme se na stejný fragment kódu:
matice = np.pole ([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
mul_5 = lambda x: x * 5
vectorized_mul_5 = np.vektorizovat (mul_5)
vectorized_mul_5 (matice)
Abychom pochopili, jak kód funguje, podíváme se na výstup zde:

Ve výše uvedeném fragmentu kódu jsme použili funkci vektorizace, která je součástí knihovny NumPy, k transformaci jednoduché definice lambda na funkci, která dokáže zpracovat každý prvek vektoru. Je důležité si uvědomit, že vektorizace je jen smyčka přes prvky a nemá to žádný vliv na výkonnost programu. NumPy také umožňuje vysílání, což znamená, že místo výše uvedeného komplexního kódu jsme mohli jednoduše udělat:
matice * 5A výsledek by byl úplně stejný. Nejprve jsem chtěl ukázat složitou část, jinak byste sekci přeskočili!
Průměr, odchylka a směrodatná odchylka
S NumPy je snadné provádět operace související s popisnou statistikou vektorů. Průměr vektoru lze vypočítat jako:
np.průměr (matice)Rozptyl vektoru lze vypočítat jako:
np.var (matice)Směrodatnou odchylku vektoru lze vypočítat jako:
np.std (matice)Zde je uveden výstup výše uvedených příkazů na danou matici:

Transpozice matice
Transpozice je velmi běžná operace, o které uslyšíte, kdykoli jste obklopeni maticemi. Transpozice je jen způsob, jak vyměnit sloupcové a řádkové hodnoty matice. Vezměte prosím na vědomí, že a vektor nelze transponovat jako vektor je jen soubor hodnot, aniž by byly tyto hodnoty kategorizovány do řádků a sloupců. Pamatujte, že převod vektoru řádků na vektor sloupců se neprovádí (na základě definic lineární algebry, která je mimo rozsah této lekce).
Prozatím najdeme mír pouhou transpozicí matice. Je velmi jednoduchý přístup k transpozici matice pomocí NumPy:
matice.TZde je uveden výstup výše uvedeného příkazu na danou matici:
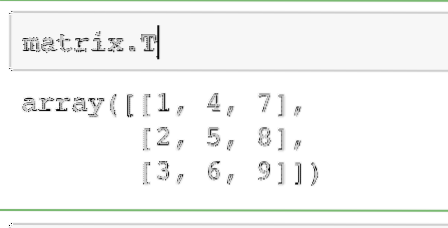
Stejnou operaci lze provést na vektoru řádku a převést jej na vektor sloupce.
Zploštění matice
Matici můžeme převést na jednorozměrné pole, pokud si přejeme zpracovat její prvky lineárně. To lze provést pomocí následujícího fragmentu kódu:
matice.zploštit ()Zde je uveden výstup výše uvedeného příkazu na danou matici:

Všimněte si, že sloučená matice je jednorozměrné pole, jednoduše lineární.
Výpočet vlastních čísel a vlastních vektorů
Vlastní vektory se velmi často používají v balíčcích Machine Learning. Když je tedy funkce lineární transformace prezentována jako matice, pak X, Eigenvectors jsou vektory, které se mění pouze v měřítku vektoru, ale ne v jeho směru. Můžeme říci, že:
Xv = γvZde je X čtvercová matice a γ obsahuje vlastní čísla. V obsahuje také vlastní vektory. S NumPy je snadné vypočítat vlastní hodnoty a vlastní vektory. Tady je fragment kódu, kde předvádíme totéž:
vyhodnocuje, evektory = np.linalg.vlastní (matice)Zde je uveden výstup výše uvedeného příkazu na danou matici:
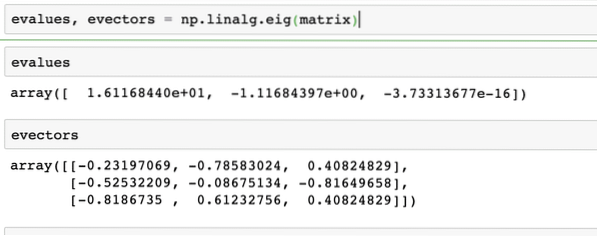
Dot produkty vektorů
Dot Products of Vectors je způsob násobení 2 vektorů. Říká vám to o kolik z vektorů je ve stejném směru, na rozdíl od křížového součinu, který vám říká opak, jak málo jsou vektory ve stejném směru (tzv. ortogonální). Můžeme vypočítat bodový produkt dvou vektorů, jak je uvedeno ve fragmentu kódu zde:
a = np.pole ([3, 5, 6])b = np.pole ([23, 15, 1])
np.tečka (a, b)
Zde je uveden výstup výše uvedeného příkazu na daná pole:

Sčítání, odečítání a násobení matic
Sčítání a odečítání více matic je v maticích docela přímá operace. Toho lze dosáhnout dvěma způsoby. Podívejme se na fragment kódu, abychom provedli tyto operace. Z důvodu zachování této jednoduchosti použijeme dvakrát stejnou matici:
np.přidat (matice, matice)Dále lze odečíst dvě matice jako:
np.odečíst (matice, matice)Zde je uveden výstup výše uvedeného příkazu na danou matici:
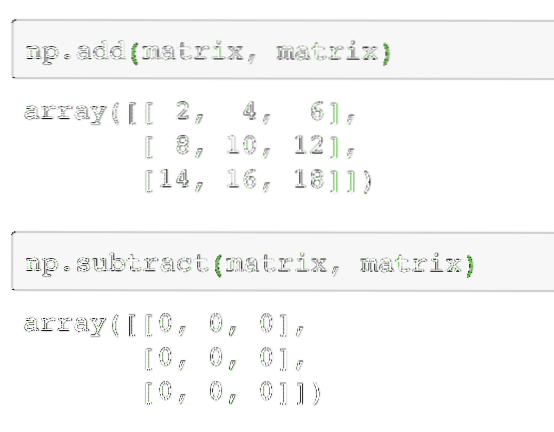
Podle očekávání je každý z prvků v matici přidán / odečten s odpovídajícím prvkem. Násobení matice je podobné hledání bodového produktu, jak jsme to udělali dříve:
np.tečka (matice, matice)Výše uvedený kód najde skutečnou hodnotu násobení dvou matic, která je uvedena jako:
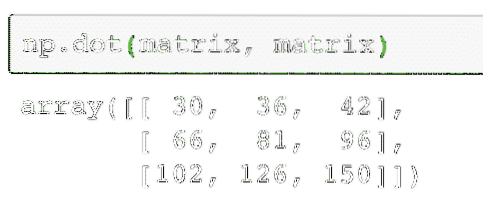
Zde je uveden výstup výše uvedeného příkazu na danou matici:

Závěr
V této lekci jsme prošli mnoha matematickými operacemi souvisejícími s vektory, maticemi a poli, které se běžně používají Zpracování dat, popisná statistika a datová věda. Jednalo se o rychlou lekci pokrývající pouze nejběžnější a nejdůležitější části široké škály konceptů, ale tyto operace by měly poskytnout velmi dobrou představu o tom, jaké všechny operace lze provádět při práci s těmito datovými strukturami.
Sdílejte prosím volně svůj názor na lekci na Twitteru s @linuxhint a @sbmaggarwal (to jsem já!).
 Phenquestions
Phenquestions